The Intuition Behind the Isomorphism Theorems

At first glance, the isomorphism theorems may seem confusing and unintuitive. The goal of this article is to hopefully give you additional insight into what the isomorphism theorems are trying to say. To make things more simple, we will only look at the theorems in the context of groups. Consider the three isomorphism theorems stated for groups.

1. Let \(G\) and \(H\) be groups and let \(\varphi: G\to H\) be a homomorphism. Then \(\ker\varphi\unlhd G\), \(\DeclareMathOperator{\im}{im} \im\varphi\le H\), and \(G/\ker\varphi\cong\im\varphi\).
2. Let \(G\) be a group, \(A\le G\), and \(B\unlhd G\). Then \(AB\le G\), \(B\unlhd AB\), \(A\cap B\unlhd A\), and \((AB)/B\cong A/(A\cap B)\).
3. Let \(G\) be a group, \(A\unlhd G\), \(B\unlhd G\), and \(A\subseteq B\). Then \(A\unlhd B\), \(B/A\unlhd G/A\), and \((G/A)/(B/A)\cong(G/B)\).

Let’s tackle each of these individually, beginning with the first one. This time, we will expand the statement of the theorem out a little.

\(\textbf{(First Isomorphism Theorem)}\) Let \(G\) and \(H\) be groups and let \(\varphi: G\to H\) be a homomorphism. Then

1. \(\ker\varphi\unlhd G\)
2. \(\im\varphi\le H\)

and \[G/\ker\varphi\cong\im\varphi\]

The essence of this theorem is the last result: \(G/\ker\varphi\cong\im\varphi\). We can think of the two previous results as stepping stones that allow us to state this last result: the first condition allows us to construct \(G/\ker\varphi\) since we can only mod out by normal subgroups and the second condition can be thought of as a sanity check to ensure that our homomorphism maps into some group, which here happens to be a subgroup in \(H\).

So what is this theorem trying to say and why is this true? Essentially, this theorem allows us to convert any homomorphism into an isomorphism, an incredibly useful tool. To see how the isomorphism is constructed, we may first look at a visual representation of \(G\) and \(\varphi\).

The elements of \(G\) can first be thought of as a collection of dots, which are then sorted into buckets by \(\varphi\) based on where they are mapped to in \(H\). Note that \(\varphi\) is not necessarily surjective.

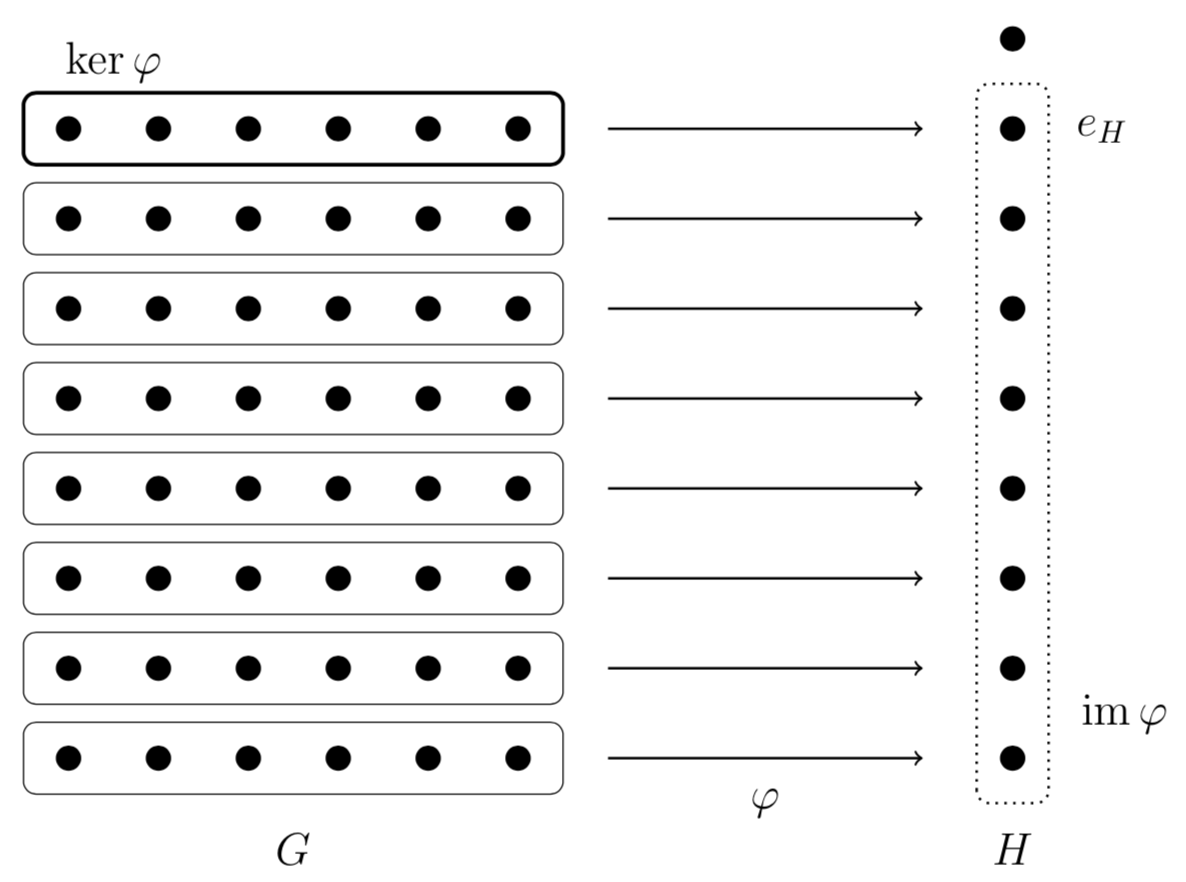
Note that this partitions the elements of \(G\) into cosets of \(\ker\varphi\) because the elements that map to the identity \(e_H\) in \(H\) is by definition \(\ker\varphi\). The key insight here is that we can interpret \(\varphi\) in a way that gives us a bijection. Let’s take a look at this picture:

While \(\varphi\) tells us for each element \(h\in\im\varphi\) which set of elements \(g\in G\) map to \(h\) (as shown in the top of the figure), we can reinterpret it as for each element \(h\in\im\varphi\) which coset \(g(\ker\varphi)\in G/\ker\varphi\) maps to \(h\) (as shown in the bottom of the figure). Since for each element in \(h\in\im\varphi\), we can only have one coset map to \(h\), we have a bijection between the cosets of \(\ker\varphi\) and the elements of \(\im\varphi\). This bijection is in fact an isomorphism. Since the cosets of \(\ker\varphi\) form the quotient group \(G/\ker\varphi\), we have the isomorphism \(G/\ker\varphi\cong\im\varphi\) as desired.

In summary, modding out by the kernel takes care of injectivity by combining the set of elements in \(G\) that map to the same element in \(H\) into a single unit, a coset, and using the image takes care of surjectivity by throwing out the elements in \(H\) not mapped to by \(\varphi\).

Let’s move on to the second isomorphism theorem.

\(\textbf{(Second Isomorphism Theorem)}\) Let \(G\) be a group, \(A\le G\), and \(B\unlhd G\). Then

1. \(AB\le G\)
2. \(B\unlhd AB\)
3. \(A\cap B\unlhd A\)

and \[(AB)/B\cong A/(A\cap B)\]

We see that similar to the first isomorphism theorem, the essence of the second isomorphism theorem is found in the last result \((AB)/B\cong A/(A\cap B)\). As with the last theorem, the first three results of the second isomorphism theorem can be thought of stepping stones for our bigger result. The first result tells us that \(AB\) is a group inside \(G\) and the next two results allow us to take the quotients \((AB)/B\) and \(A/(A\cap B)\) since we can only mod out by normal subgroups.

We again think of the elements of \(G\) as a collection of dots. This time, we focus on the subgroup \(AB\) and we partition its elements into cosets of \(A\) and \(B\). Since \(B\) is normal, we can consider some homomorphism \(\varphi\) that has \(B\) as its kernel. This gives us the following diagram.

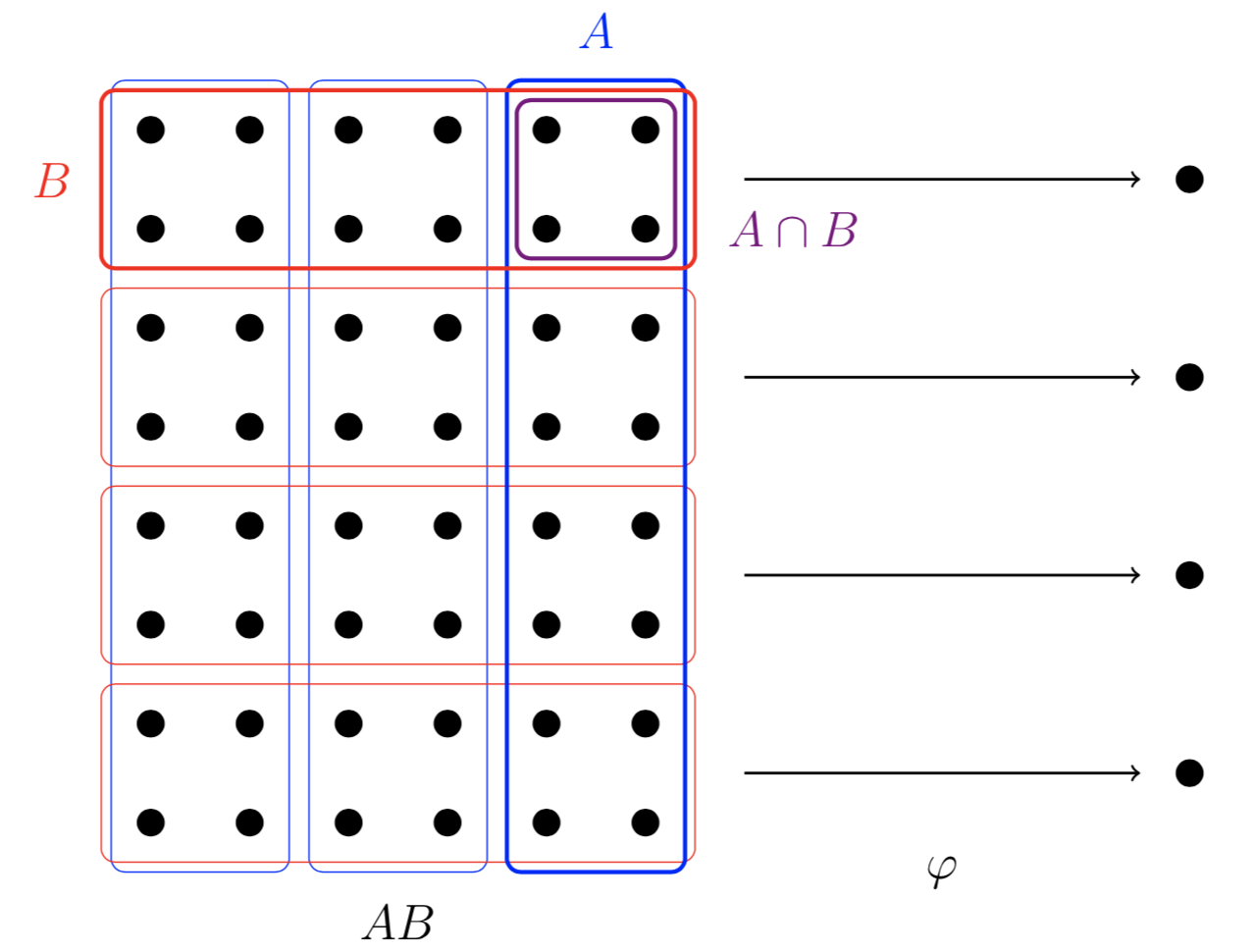
The key insight here is that we can interpret this map \(\varphi\) two different ways. If we look only look at \(AB\) and \(B\), we see that this map looks like \((AB)/B\). If we look only at \(A\) and \(A\cap B\), we see that this map look like \(A/(A\cap B)\). The following diagram makes this more explicit.

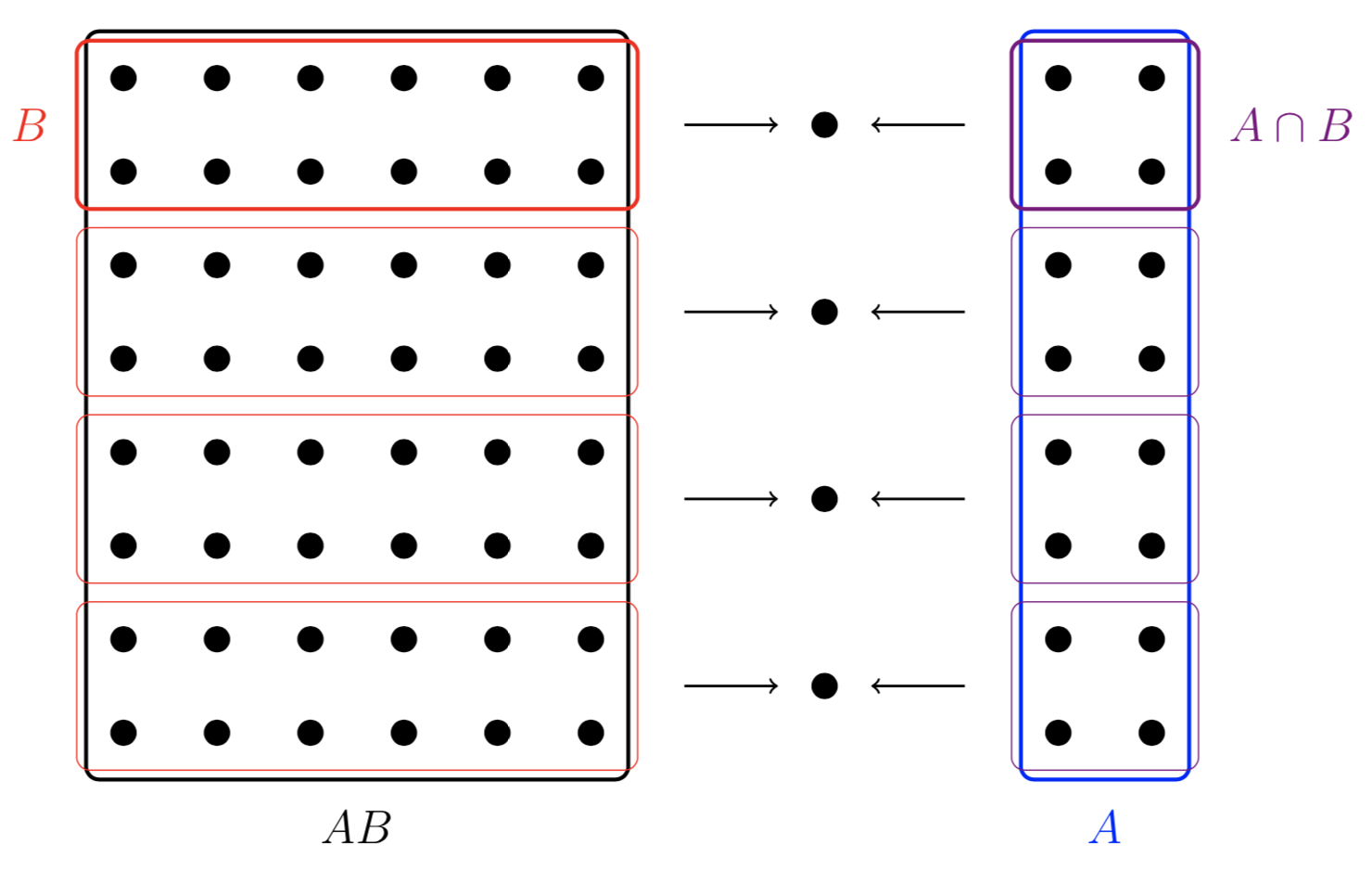
Thus, we have the isomorphism \((AB)/B\cong A/(A\cap B)\) as desired.

Finally, we look at the third isomorphism theorem.

\(\textbf{(Third Isomorphism Theorem)}\) Let \(G\) be a group, \(A\unlhd G\), \(B\unlhd G\), and \(A\subseteq B\). Then

1. \(A\unlhd B\)
2. \(B/A\unlhd G/A\)

and \[(G/A)/(B/A)\cong(G/B)\]

Again, the essence of this theorem is the last result \((G/A)/(B/A)\cong(G/B)\). The previous two results \(A\unlhd B\) and \(B/A\unlhd G/A\) are needed to construct the quotients \(B/A\) and \((G/A)/(B/A)\) since we can only mod out by normal subgroups.

We will again think of the elements of \(G\) as a collection of dots. Then we look at the cosets of \(A\) and \(B\).

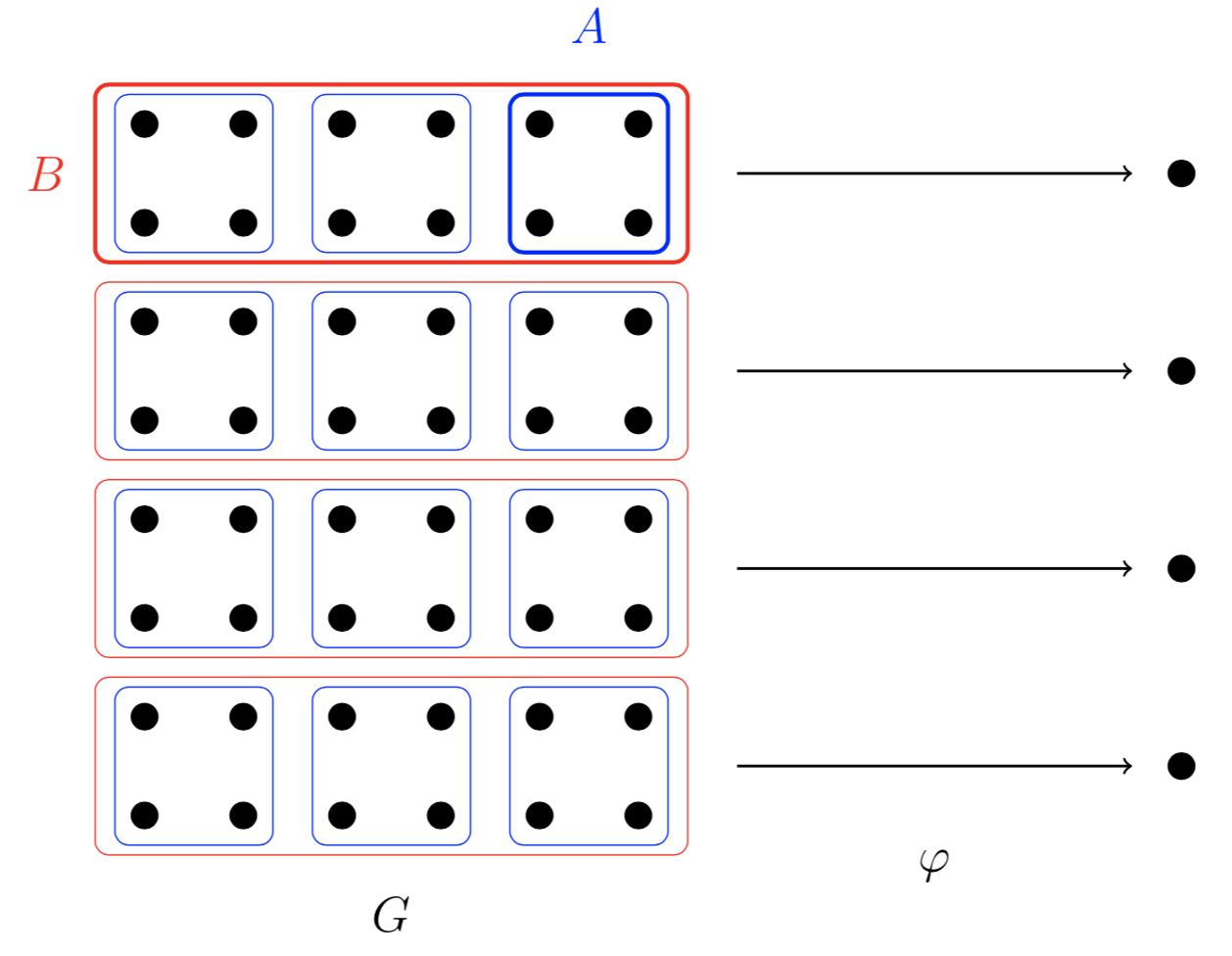
If we just look at \(G\) and \(B\), we see that this homomorphism \(\varphi\) gives us \(G/B\). The key insight here is that we can mod the whole picture by \(A\) and everything still ‘works’.

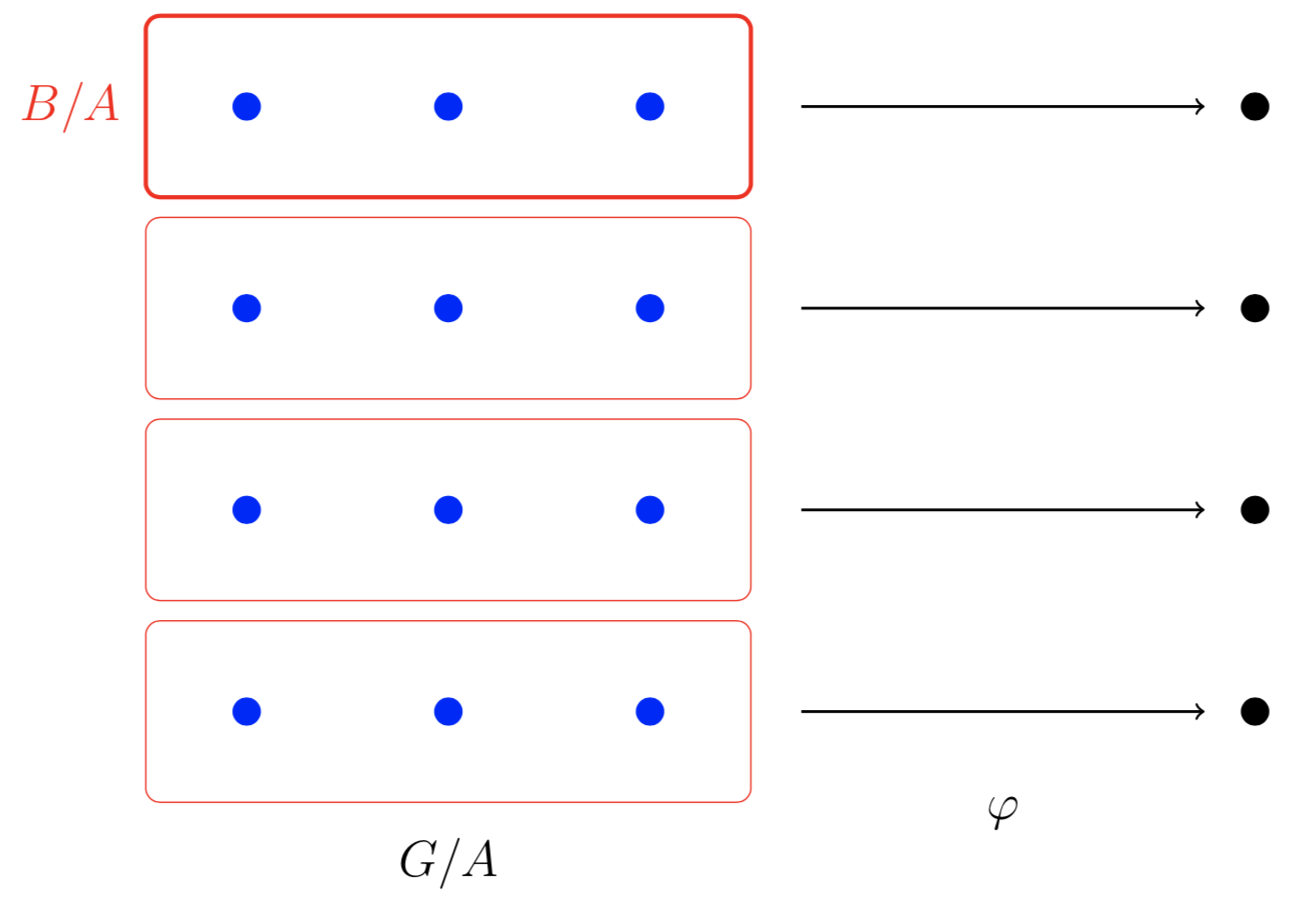
Here, each blue dot represents a coset of \(A\) instead of an element of \(G\). Thus, the set of all blue dots forms the group \(G/A\) and the solid red box now represents \(B/A\) instead of \(B\). Our homomorphism \(\varphi\) now represents \((G/A)/(B/A)\). Thus, we have \((G/A)/(B/A)\cong(G/B)\) as desired.

Hopefully, this article was able to help you understand and appreciate the isomorphism theorems more.